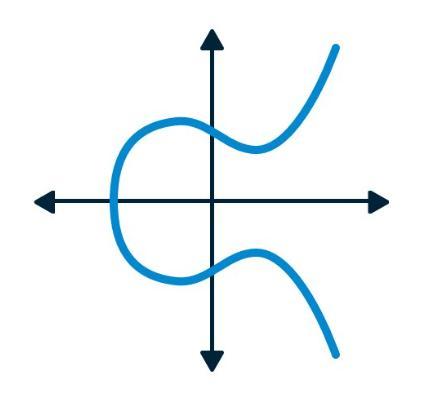
- an elliptic curve is the set of solutions to a Weierstrass equation:
The term
- Any solution that satisfies the right side of the equation has 2 solutions: +ve and -ve
- For Elliptic Curve Cryptography (ECC) we study the elliptic curves over a finite field
- i.e.
- thus, we can think of an elliptic curve, , as the set of points defined by:
Common Elliptic Curves in Blockchain
Addition
- An addition has the following properties:
- (commutative)
- Since point addition is commutative, it is considered an Abelian Group
- General steps for addition:
- Since the curve is over a finite field, these operations should be:
- modulo p
- instead of division, should multiply by the modular inverse
- ,
- Since the curve is over a finite field, these operations should be:
Point Negation
- for elliptic point , its negation point
Scalar Multiplication
- General steps for scalar multiplication:
input: P in E(Fp) and an integer n > 0Set Q = P and R = O.Loop while n > 0:If n ≡ 1 mod 2, set R = R + Q.Set Q = 2 Q and n = ⌊n/2⌋.If n > 0, continue with the loop in Step 2.
Return the point R, which equals nP.
Inversion
- given , find such that
Coordinate System
- Elliptic curve operations over a finite field include (as above):
- addition (fast)
- multiplication (slower)
- inversion (extremely slow)
- Affine Coordinates is the native coordinate system for ECC
Affine
- inversion needed for every point addition or multiplication
Projective
- The number of modular additions and multiplications increases, though they’re quick
- Will need to convert back to affine at the end so that it will involve one inversion
Affine vs Projective
- Projective which involves only one inversion at the end is usually much faster than affine which requires inversion at every addition and multiplication
- in ZK, the cost of inversion is the same as multiplication (i.e. given , prove ). Thus, it’s better to use affine coordinates