Elliptic Curves - Overview

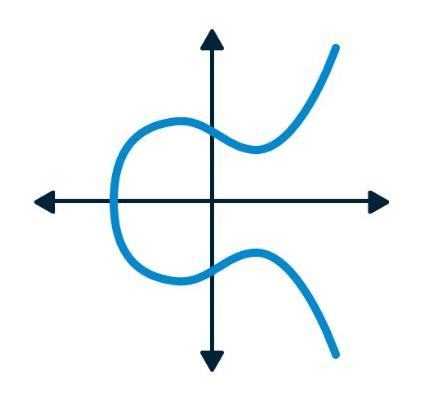
• an elliptic curve $E$ is the set of solutions to a Weierstrass equation:

$$\begin{array}{rl}{y}^2=x^3+ax+b\text{where }& 4a^3+27b^2\ne 0\\ & \text{point at infinity}=0\end{array}$$

The $y^2$ term

• Any solution that satisfies the right side of the equation has 2 $y$ solutions: +ve and -ve

• For Elliptic Curve Cryptography (ECC) we study the elliptic curves over a finite field $F_p$
  • i.e. $y^2=x^3+ax+b(modp)$
• thus, we can think of an elliptic curve, $E$, as the set of points defined by:

$$\begin{array}{r}E(Fp)=(x,y):x,y\in Fp\text{satisfying }{y}^2=x^3+ax+b\cup O\end{array}$$

Common Elliptic Curves in Blockchain

• secp256k1
• BN254
• BLS12-381
• Curve25519

Addition

• An addition has the following properties:
  1. $P+O=O+P=P$
  2. $P+(-P)=O$
  3. $(P+Q)+R=P+(Q+R)$
  4. $P+Q=Q+P$ (commutative)
• Since point addition is commutative, it is considered an Abelian Group
• General steps for addition:
  • Since the curve is over a finite field, these operations should be:
    • modulo p
    • instead of division, should multiply by the modular inverse
  1. $\text{if }P\ne Q$ $\lambda =(y_2-y_1)/(x_2-x_1)$
  2. $\text{if }P=Q$ $\lambda =(3x_1^2+a)/2y_1$
  3. $x_3={\lambda }^2-x_1-x_2$ , $y_3=\lambda (x_1-x_3)-y_1$
  4. $P+Q=(x_3,y_3)$

Point Negation

• for elliptic point $Ppx,py$, its negation point $Q=-P=\{p_x,-p_y\}=\{p_x,modulus-p_y\}$

Scalar Multiplication

• $3P=P+P+P$
• General steps for scalar multiplication:
  1. input: P in E(Fp) and an integer n > 0
  2. Set Q = P and R = O.
  3. Loop while n > 0:
     1. If n ≡ 1 mod 2, set R = R + Q.
     2. Set Q = 2 Q and n = ⌊n/2⌋.
     3. If n > 0, continue with the loop in Step 2.
  4. Return the point R, which equals nP.

Inversion

• given $a$, find $b$ such that $a\cdot b\equiv 1(modp)$

Coordinate System

• Elliptic curve operations over a finite field include (as above):
  • addition (fast)
  • multiplication (slower)
  • inversion (extremely slow)
• Affine Coordinates is the native coordinate system for ECC

Affine

• inversion needed for every point addition or multiplication

Projective

• The number of modular additions and multiplications increases, though they’re quick
• Will need to convert back to affine at the end so that it will involve one inversion

Affine vs Projective

• Projective which involves only one inversion at the end is usually much faster than affine which requires inversion at every addition and multiplication
• in ZK, the cost of inversion is the same as multiplication (i.e. given $x=a/b$, prove $x\ast b==a$). Thus, it’s better to use affine coordinates